Author
Affiliation

Alex Kaizer

University of Colorado-Anschutz Medical Campus

This page is part of the University of Colorado-Anschutz Medical Campus’ BIOS 6618 Labs collection, the mini-lecture content delivered at the start of class before breaking out into small groups to work on the homework assignment.

What’s on the docket this week?

In Week 4 we are providing examples of coding in R for power calculations in different settings. We will also further introduce the use of the ggplot2 package for creating plots of our power calculations.

The ggplot2 Package

The ggplot2 package helps to implement the “Grammar of Graphics” in R. It provides a nice framework for generating graphics that share a common structure (i.e., so you don’t have to refresh yourself on how 20 different graphics functions work with different arguments, settings, etc.). Like anything in R, though, it can have a bit of a steep learning curve.

We aren’t going to delve too deeply into nitty-gritty of ggplot() (at least not in this lab), but there are a variety of sources out there that provide information on how to use and set-up plotting with ggplot2:

One function that can help in applying the ggplot() function is the qplot() function, which serves as wrapper shortcut for those more familiar with building graphics with the base plot() function. You’ll see it used below for creating our plots.

Using R for Power and Sample Size

We will consider different scenarios for testing a single mean (i.e., using a one-sample Z-test or a one-sample t-test with \(H_0: \mu_0 = 0\)):

  1. \(\sigma=10\) (known);\(N=15,20,25\); detectable difference between null and alternative means from -15 to 15; \(\alpha=0.01,0.05,0.10\) (two-sided). Find the power.

  2. \(s=10\) (\(\sigma\) unknown);\(N=15,20,25\); detectable difference between null and alternative means from -15 to 15; \(\alpha=0.01,0.05,0.10\) (two-sided). Find the power.

  3. \(s=10\) (\(\sigma\) unknown); detectable difference between null and alternative means from 5 to 10; \(\alpha=0.01,0.05,0.10\) (two-sided); \(1-\beta=\text{Power}=0.80,0.90,0.95\). Find N.

  4. \(s=10\) (\(\sigma\) unknown); \(N=15,20,25\), \(\alpha=0.01,0.05,0.10\) (two-sided); \(1-\beta=\text{Power}=0.80,0.90,0.95\). Find the detectable difference between null and alternative means.

For each scenario we will plot our values using the ggplot2 package to visualize the differences across all the combinations.

Scenario 1 - Known \(\sigma\), Find Power

\(\sigma=10\) (known);\(N=15,20,25\); detectable difference between null and alternative means from -15 to 15; \(\alpha=0.01,0.05,0.10\) (two-sided). Find the power.

From our lecture slides we know that

\[ Z_{1-\beta} = \frac{|\mu_0 - \mu_1|}{se(\bar{X})} - Z_{1-\frac{\alpha}{2}} \]

However, in this form we have to do a few more steps to get the power and not just \(Z_{1-\beta}\) (i.e., the value of the Z-statistic from our standard normal distribution that is at the given level of power):

\[ 1-\beta = \Phi\left[ \frac{|\mu_0 - \mu_1|}{\sigma / \sqrt{n}} - Z_{1-\frac{\alpha}{2}} \right] \]

In R it is easiest to program our own function from the equations provided in this lecture to calculate the power for our two-sided Z:

Code 
# Write function to calculate the power given the detectable difference, SD, N, and alpha
findPowerZ <- function(diff = 5, sd = 1, n = 10, alpha = 0.05) { 
    z.alpha <- qnorm(1 - (alpha/2))
    power <- pnorm( abs(diff) / (sd/sqrt(n) ) - z.alpha)
    return(power)
}

For example, we can calculate what our power would be if we observed a detectable difference of either 5 or -5 when \(\sigma=10\), \(N=20\), \(\alpha=0.05\):

Code 
# Calculate power for a detectable difference of 5
findPowerZ( diff=5, sd=10, n=20, alpha=0.05)
[1] 0.6087659
Code 
# Calculate power for a detectable difference of -5
findPowerZ( diff=-5, sd=10, n=20, alpha=0.05)
[1] 0.6087659

Note that they result in the same power because the normal distribution is symmetric and we assume that \(H_0: \mu_0=0\).

We can leverage the expand.grid() function to more easily identify all combinations of \(n\), \(\alpha\), and our detectable difference (279 in total) to then loop through and calculate the power:

Code 
# Set standard deviation at desired value and create data frame with expand.grid for all combinations of parameters of interest
stdev <- 10
powers <- expand.grid(n=c(15,20,25), alpha=c(0.01,0.05,0.1), diff=(-15:15))

# Create new column to save results of power
powers$power <- NA

# Loop through each row (i.e., combination) and calculate the power achieved
for(i in 1:nrow(powers)){ 
    p <- findPowerZ(n = powers$n[i], alpha = powers$alpha[i], diff = powers$diff[i], sd = stdev)
    powers$power[i] <- p
}

# View the first 6 rows
head(powers)
   n alpha diff     power
1 15  0.01  -15 0.9993889
2 20  0.01  -15 0.9999820
3 25  0.01  -15 0.9999996
4 15  0.05  -15 0.9999408
5 20  0.05  -15 0.9999990
6 25  0.05  -15 1.0000000

We may remember that some functions in R are able to handle vectorized arguments (i.e., instead of looping through a vector of values of interest it can automatically calculate across all values in the vector). Here we see that skipping the for loop with our findPowerZ function results in the same power estimates:

Code 
# Since our findPowerZ function uses R functions that can take vectors for their arguments, we can bypass the loop and just use our respective columns to calculate the power without a for loop:

powers$power_vectorize <- findPowerZ(n = powers$n, alpha = powers$alpha, diff = powers$diff, sd = stdev)

# check that all powers are equal (should all be TRUE)
table(powers$power == powers$power_vectorize)

TRUE 
 279

Now that we’ve calculated the expected power for each of the 279 combinations, we can work on plotting them in one figure. For this example we will plot our desired measure, power, on the y-axis, and the detectable difference on the x-axis.

The figure will be somewhat busy, but we can help differentiate the various combinations with different line colors, line styles, and types of points. One extra step we need to complete is to tell R we want to treat n and alpha as factors, because as their numeric values ggplot() will return errors.

Code 
# load the ggplot2 package
library(ggplot2)

# To take advantage of the linetype, color, and shape arguments with our current data frame we need to coerce the values into factors
powers$n <- as.factor(powers$n)
powers$alpha <- as.factor(powers$alpha)

# Plot the resulting power curves
qplot(diff, power, data = powers, linetype = n, color = alpha, geom = "line",shape = n) +
    geom_point() + # add points to plot
  theme_bw() + # change plotting aesthetic/style to have black/white background with grid
  xlab("Difference") + ylab("Power") + # change axis labels
    ggtitle("Achievable Power vs. Difference of Means by Sample Size (N) and Alpha")
Warning: `qplot()` was deprecated in ggplot2 3.4.0.

From this figure we can make various insights, a few of which are highlighted below:

  • When we evaluate the power at \(H_0\), what we actually have summarized is the type I error rate. We can roughly observe this since the colored lines achieve the approximate \(\alpha\) value when the difference is 0. Alternatively, we can look at our powers data frame to review the resulting power when the difference is 0. (Strictly speaking, since we were calculating power, we actually have calculated \(\frac{\alpha}{2}\)…but we could solve the equation for \(Z_{1-\alpha/2}\) to then solve for \(\alpha\) precisely.)
  • We can see that as \(\alpha\) increases we have higher power, holding \(n\) and the difference constant. This makes sense given the trade off of \(\alpha\) and \(\beta\) (our type I and type II errors).
  • Similar, as \(n\) increases we have higher power.
  • We can see the combinations where we wouldn’t have desirable power (e.g., <80%).

Equivalent of qplot

We can also just use the direct ggplot functions instead of its quick plotting shortcut function:

Code 
# To take advantage of the linetype, color, and shape arguments with our current data frame we need to coerce the values into factors
powers$n <- as.factor(powers$n)
powers$alpha <- as.factor(powers$alpha)

# Plot the resulting power curves
ggplot(data=powers, aes(x=diff, y=power, color=alpha, shape=n, linetype=n)) +
  geom_line() +
    geom_point() + 
  theme_bw() + 
  xlab("Difference") + ylab("Power") +
    ggtitle("Achievable Power vs. Difference of Means by Sample Size (N) and Alpha")

Scenario 2 - Unknown \(\sigma\), Find Power

\(s=10\) (\(\sigma\) unknown);\(N=15,20,25\); detectable difference between null and alternative means from -15 to 15; \(\alpha=0.01,0.05,0.10\) (two-sided). Find the power.

In this case we know that there are existing functions we can leverage to calculate our power, such as power.t.test():

Code 
pwrt_b <- power.t.test(n = 15, sd = 10, sig.level = 0.01, delta = -15, type = "one.sample", alternative = "two.sided")
pwrt_b # print the results

     One-sample t test power calculation 

              n = 15
          delta = 15
             sd = 10
      sig.level = 0.01
          power = 0.9937996
    alternative = two.sided
Code 
pwrt_b$power # specifically print the estimated power
[1] 0.9937996

We can essentially take our code from Scenario 1 above and replace the function with power.t.test to create our figure:

Code 
# Set standard deviation at desired value and create data frame with expand.grid for all combinations of parameters of interest
stdev <- 10
powers2 <- expand.grid(n=c(15,20,25), alpha=c(0.01,0.05,0.1), diff=(-15:15))

# Create new column to save results of power
powers2$power <- NA

# Loop through each row (i.e., combination) and calculate the power achieved
for(i in 1:nrow(powers2)){ 
    p <- power.t.test(n = powers2$n[i], sig.level = powers2$alpha[i], delta = powers2$diff[i], sd = stdev, power = NULL, 
                      type = 'one.sample', alternative = 'two.sided')
    powers2$power[i] <- p$power
}
Code 
# load the ggplot2 package (in case you hadn't already)
library(ggplot2)

# To take advantage of the linetype, color, and shape arguments with our current data frame we need to coerce the values into factors
powers2$n <- as.factor(powers2$n)
powers2$alpha <- as.factor(powers2$alpha)

# Plot the resulting power curves
qplot(diff, power, data = powers2, linetype = n, color = alpha, geom = "line",shape = n) +
    geom_point() + theme_bw() + xlab("Difference") + ylab("Power") +
    ggtitle("Achievable Power vs. Difference of Means by Sample Size (N) and Alpha")

We see similar results to Scenario 1, however we can see that for each combination, we have generally lower power than in Scenario 1. This is a result of the difference between assuming known versus unknown standard deviation.

Can power.t.test Take Vectors

The power.t.test function is able to handle our vectorized data, but we can see that it returns multiple values from the function the we could reference:

Code 
names(pwrt_b)
[1] "n"           "delta"       "sd"          "sig.level"   "power"      
[6] "alternative" "note"        "method"

So we can extract whatever information we find most relevant:

Code 
# Extract only the power
pwrt_b$power
[1] 0.9937996
Code 
# Extract only the delta
pwrt_b$delta
[1] 15
Code 
# Extract both power and delta
pwrt_b[c('power','delta')]
$power
[1] 0.9937996

$delta
[1] 15
Code 
# Extract both power and delta, but force it to be a vector and not a list
unlist(pwrt_b[c('power','delta')])
     power      delta 
 0.9937996 15.0000000

If we just put in our vectors we get all of the quantities returned:

Code 
stdev <- 10
powers2_vec <- expand.grid(n=c(15,20,25), alpha=c(0.01,0.05,0.1), diff=(-15:15))

pwrt_vectorized <- power.t.test(n = powers2_vec$n, 
                                sig.level = powers2_vec$alpha, 
                                delta = powers2_vec$diff, 
                                sd = stdev, 
                                power = NULL, 
                                type = 'one.sample', 
                                alternative = 'two.sided')
pwrt_vectorized

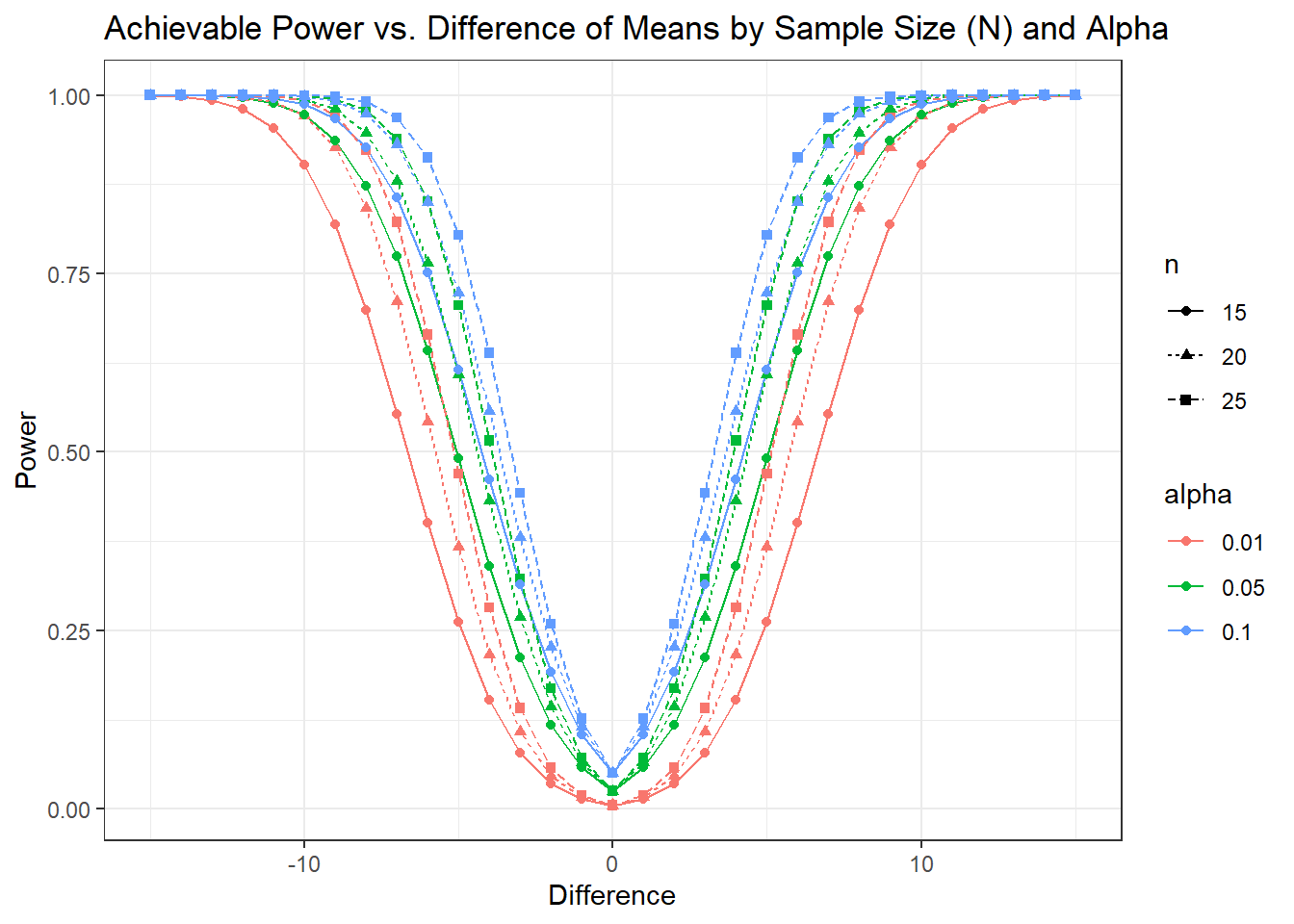
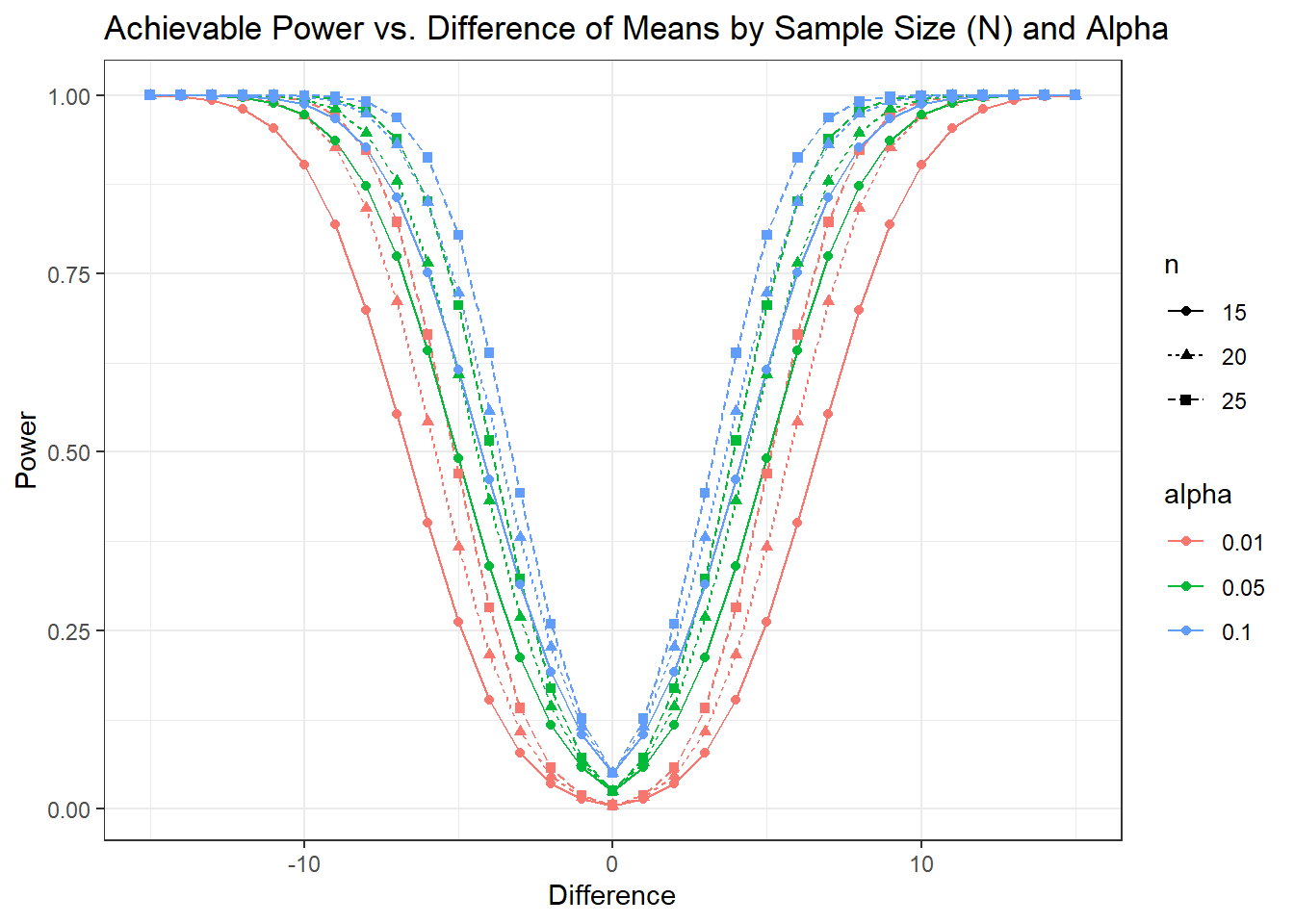
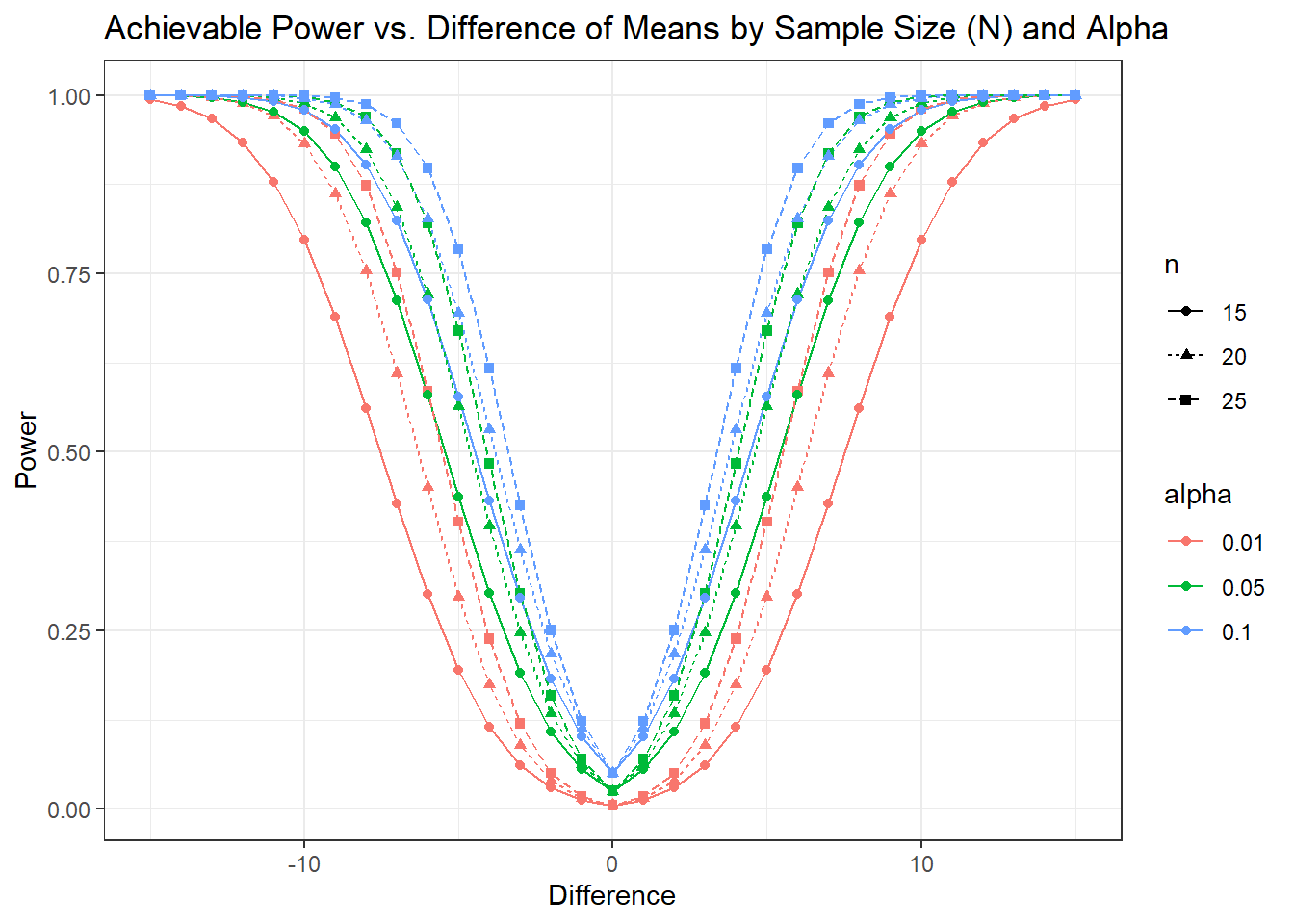
     One-sample t test power calculation 

              n = 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25, 15, 20, 25
          delta = 15, 15, 15, 15, 15, 15, 15, 15, 15, 14, 14, 14, 14, 14, 14, 14, 14, 14, 13, 13, 13, 13, 13, 13, 13, 13, 13, 12, 12, 12, 12, 12, 12, 12, 12, 12, 11, 11, 11, 11, 11, 11, 11, 11, 11, 10, 10, 10, 10, 10, 10, 10, 10, 10, 9, 9, 9, 9, 9, 9, 9, 9, 9, 8, 8, 8, 8, 8, 8, 8, 8, 8, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5, 5, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15
             sd = 10
      sig.level = 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10, 0.01, 0.01, 0.01, 0.05, 0.05, 0.05, 0.10, 0.10, 0.10
          power = 0.99379964, 0.99977175, 0.99999374, 0.99968449, 0.99999414, 0.99999991, 0.99994334, 0.99999923, 0.99999999, 0.98492058, 0.99904610, 0.99995370, 0.99890204, 0.99996285, 0.99999894, 0.99976298, 0.99999400, 0.99999987, 0.96672386, 0.99656180, 0.99971913, 0.99659928, 0.99980079, 0.99998997, 0.99912482, 0.99996071, 0.99999843, 0.93326751, 0.98929560, 0.99860140, 0.99061448, 0.99909540, 0.99992373, 0.99714477, 0.99978391, 0.99998523, 0.87812317, 0.97115118, 0.99427099, 0.97688373, 0.99651570, 0.99953252, 0.99175854, 0.99900034, 0.99988907, 0.79670393, 0.93249537, 0.98063807, 0.94908647, 0.98859129, 0.99768460, 0.97891618, 0.99610286, 0.99933233, 0.68910390, 0.86228289, 0.94578357, 0.89945099, 0.96815164, 0.99070503, 0.95208492, 0.98716538, 0.99677194, 0.56192862, 0.75363390, 0.87346165, 0.82130998, 0.92389872, 0.96963105, 0.90297615, 0.96417280, 0.98741901, 0.42761072, 0.61050606, 0.75174714, 0.71289906, 0.84350550, 0.91877622, 0.82425706, 0.91484955, 0.96028374, 0.30095252, 0.45011623, 0.58571735, 0.58040966, 0.72100197, 0.82072129, 0.71377695, 0.82663952, 0.89776394, 0.19441072, 0.29734431, 0.40227469, 0.43784659, 0.56448290, 0.66970136, 0.57805549, 0.69514934, 0.78338612, 0.11453654, 0.17375617, 0.23822547, 0.30284108, 0.39686955, 0.48396689, 0.43215762, 0.53181412, 0.61725900, 0.06121551, 0.08891184, 0.11957051, 0.19037733, 0.24648577, 0.30161925, 0.29495606, 0.36277965, 0.42572891, 0.02954918, 0.03952378, 0.05021130, 0.10800411, 0.13348840, 0.15876192, 0.18211929, 0.21707518, 0.25048467, 0.01283438, 0.01516757, 0.01747061, 0.05498090, 0.06241123, 0.06948589, 0.10098691, 0.11249211, 0.12326268, 0.00500000, 0.00500000, 0.00500000, 0.02500000, 0.02500000, 0.02500000, 0.05000000, 0.05000000, 0.05000000, 0.01283438, 0.01516757, 0.01747061, 0.05498090, 0.06241123, 0.06948589, 0.10098691, 0.11249211, 0.12326268, 0.02954918, 0.03952378, 0.05021130, 0.10800411, 0.13348840, 0.15876192, 0.18211929, 0.21707518, 0.25048467, 0.06121551, 0.08891184, 0.11957051, 0.19037733, 0.24648577, 0.30161925, 0.29495606, 0.36277965, 0.42572891, 0.11453654, 0.17375617, 0.23822547, 0.30284108, 0.39686955, 0.48396689, 0.43215762, 0.53181412, 0.61725900, 0.19441072, 0.29734431, 0.40227469, 0.43784659, 0.56448290, 0.66970136, 0.57805549, 0.69514934, 0.78338612, 0.30095252, 0.45011623, 0.58571735, 0.58040966, 0.72100197, 0.82072129, 0.71377695, 0.82663952, 0.89776394, 0.42761072, 0.61050606, 0.75174714, 0.71289906, 0.84350550, 0.91877622, 0.82425706, 0.91484955, 0.96028374, 0.56192862, 0.75363390, 0.87346165, 0.82130998, 0.92389872, 0.96963105, 0.90297615, 0.96417280, 0.98741901, 0.68910390, 0.86228289, 0.94578357, 0.89945099, 0.96815164, 0.99070503, 0.95208492, 0.98716538, 0.99677194, 0.79670393, 0.93249537, 0.98063807, 0.94908647, 0.98859129, 0.99768460, 0.97891618, 0.99610286, 0.99933233, 0.87812317, 0.97115118, 0.99427099, 0.97688373, 0.99651570, 0.99953252, 0.99175854, 0.99900034, 0.99988907, 0.93326751, 0.98929560, 0.99860140, 0.99061448, 0.99909540, 0.99992373, 0.99714477, 0.99978391, 0.99998523, 0.96672386, 0.99656180, 0.99971913, 0.99659928, 0.99980079, 0.99998997, 0.99912482, 0.99996071, 0.99999843, 0.98492058, 0.99904610, 0.99995370, 0.99890204, 0.99996285, 0.99999894, 0.99976298, 0.99999400, 0.99999987, 0.99379964, 0.99977175, 0.99999374, 0.99968449, 0.99999414, 0.99999991, 0.99994334, 0.99999923, 0.99999999
    alternative = two.sided

Fortunately this is easily solved by either [1] just extracting the power object in the results or [2] adding $power to our function so it only return those values:

Code 
# Extract results from output dump
powers2_vec$power <- pwrt_vectorized$power

# Rerun power.t.test to only save power
powers2_vec$power_v2 <- power.t.test(n = powers2_vec$n, 
                                sig.level = powers2_vec$alpha, 
                                delta = powers2_vec$diff, 
                                sd = stdev, 
                                power = NULL, 
                                type = 'one.sample', 
                                alternative = 'two.sided')$power

# check that everything matches the for loop above
table(powers2$power == powers2_vec$power)

TRUE 
 279
Code 
table(powers2$power == powers2_vec$power_v2)

TRUE 
 279

Scenario 3 - Unknown \(\sigma\), Find N

\(s=10\) (\(\sigma\) unknown); detectable difference between null and alternative means from 5 to 10; \(\alpha=0.01,0.05,0.10\) (two-sided); \(1-\beta=\text{Power}=0.80,0.90,0.95\). Find N.

We again can modify our code from above to solve for the sample size needed. But first let’s examine how we can extract the needed sample size and round up to the next whole number with the ceiling() function:

Code 
pwrt_c <- power.t.test(power=0.8, sd = 10, sig.level = 0.01, delta = 5, type = "one.sample", alternative = "two.sided")
pwrt_c # view all output

     One-sample t test power calculation 

              n = 50.0647
          delta = 5
             sd = 10
      sig.level = 0.01
          power = 0.8
    alternative = two.sided
Code 
ceiling(pwrt_c$n) # only extract the needed N and round up to the next whole number
[1] 51

We see that our estimate here is rounded up from 50.0646962 to be 51.

Now let’s modify our code from Scenario 2 to solve for \(N\) over differences from 5 to 10 in increments of 0.1:

Code 
# Set standard deviation at desired value and create data frame with expand.grid for all combinations of parameters of interest
stdev <- 10
sampsize_df <- expand.grid(power=c(0.8,0.9,0.95), alpha=c(0.01,0.05,0.1), diff=seq(5,10,by=0.1) )

# Create new column to save results of N
sampsize_df$n <- NA

# Loop through each row (i.e., combination) and calculate the power achieved
for(i in 1:nrow(sampsize_df)){ 
    p <- power.t.test(n = NULL, sig.level = sampsize_df$alpha[i], delta = sampsize_df$diff[i], sd = stdev, 
                      power = sampsize_df$power[i], type = 'one.sample', alternative = 'two.sided')
    sampsize_df$n[i] <- ceiling( p$n )
}

# load the ggplot2 package (in case you hadn't already)
library(ggplot2)

# To take advantage of the linetype, color, and shape arguments with our current data frame we need to coerce the values into factors
sampsize_df$power <- as.factor(sampsize_df$power)
sampsize_df$alpha <- as.factor(sampsize_df$alpha)

# Plot the resulting power curves
qplot(diff, n, data = sampsize_df, linetype = power, color = alpha, geom = "line",shape = power) +
    geom_point() + theme_bw() + xlab("Difference") + ylab("Required Sample Size") +
    ggtitle("Required Sample Size (N) vs. Difference of Means by Power and Alpha")

From this figure we can take away the conclusion that smaller detectable differences lead to a larger sample size to achieve a desired power, type I error rate, and SD.

Scenario 4 - Unknown \(\sigma\), Find Detectable Difference

\(s=10\) (\(\sigma\) unknown); \(N=15,20,25\), \(\alpha=0.01,0.05,0.10\) (two-sided); \(1-\beta=\text{Power}=0.80,0.90,0.95\). Find the detectable difference between null and alternative means.

Again, we can modify our earlier set-up from Scenarios 2 and 3 to address this question:

Code 
pwrt_d <- power.t.test(power=0.8, sd = 10, sig.level = 0.01, n=15, type = "one.sample", alternative = "two.sided")
pwrt_d # view the output

     One-sample t test power calculation 

              n = 15
          delta = 10.03483
             sd = 10
      sig.level = 0.01
          power = 0.8
    alternative = two.sided
Code 
pwrt_d$delta # view the detectable difference only
[1] 10.03483

Let’s modify our code to create a plot of our detectable difference across the scenarios:

Code 
# Set standard deviation at desired value and create data frame with expand.grid for all combinations of parameters of interest
stdev <- 10
diff_df <- expand.grid(n=c(15,20,25), alpha=c(0.01,0.05,0.1), power=c(0.8,0.9,0.95))

# Create new column to save results of diff
diff_df$diff <- NA

# Loop through each row (i.e., combination) and calculate the power achieved
for(i in 1:nrow(diff_df)){ 
    p <- power.t.test(n = diff_df$n[i], sig.level = diff_df$alpha[i], delta = NULL, sd = stdev, power = diff_df$power[i], 
                      type = 'one.sample', alternative = 'two.sided')
    diff_df$diff[i] <- p$delta
}

# load the ggplot2 package (in case you hadn't already)
library(ggplot2)

# To take advantage of the linetype, color, and shape arguments with our current data frame we need to coerce the values into factors
diff_df$power <- as.factor(diff_df$power)
diff_df$alpha <- as.factor(diff_df$alpha)

# Plot the resulting power curves
qplot(n, diff, data = diff_df, linetype = power, color = alpha, geom = "line",shape = power) +
    geom_point() + theme_bw() + xlab("Sample Size") + ylab("Difference in Means") +
    ggtitle("Detectable Mean Difference vs. Sample Size (N) by Power and Alpha")

In this figure we can note that for any combination of \(\alpha\) and power, the smaller our sample size is, the larger our difference in means will be that we can detect. In other words, if we wanted to detect a smaller difference in means, we would need to increase our sample size if we already set the values for \(s\), \(\alpha\), and \(1-\beta\) (power).