Week 11 Practice Problems

Author

Affiliation

Alex Kaizer

University of Colorado-Anschutz Medical Campus

This page includes optional practice problems, many of which are structured to assist you on the homework with Solutions provided on a separate page. Data sets, if needed, are provided on the BIOS 6618 Canvas page for students registered for the course.

This week’s extra practice exercises focus on the wonderfully wide world of applications for MLR: confounding, mediation, interactions, general linear hypothesis testing, and polynomial regression.

Dataset Background

All of our exercises will use the surgery timing data set (Surgery_Timing.csv) provided by the TSHS section of the American Statistical Association. We can load the data into R with the following line of code:

Code

dat <- read.csv('../../.data/Surgery_Timing.csv')

The following table summarizes the variables we will be exploring and provide brief definitions:

Variable	Code Name	Description
Risk Stratification Index (RSI) for In-Hospital Complications	`complication_rsi`	Estimated risk of having an in-hospital complication.
Day of Week	`dow`	Weekday surgery took place (1=Monday, 5=Friday)
Operation Time	`hour`	Timing of operation during the day (06:00 to 19:00)
Phase of Moon	`moonphase`	Moon phase during procedure (1=new, 2=first quarter, 3=full, 4=last quarter)
Age	`age`	Age in years
BMI	`bmi`	Body mass index (kg/m2)
AHRQ Procedure Category	`ahrq_ccs`	US Agency for Healthcare Research and Quality’s Clinical Classifications Software procedure category
Complication Observed	`complication`	In-hospital complication
Diabetes	`baseline_diabetes`	Diabetes present at baseline

Exercise 1: Confounding

We will use linear regression to examine the relationship between the outcome of RSI for in-hospital complications with surgery on a Monday/Tuesday (versus Wednesday/Thursday/Friday) and moon phase to answer the following exercises:

1a: Unadjusted Model and Interpretation

What is the unadjusted (crude) estimate for the association between RSI and day of the week? Write a brief, but complete, summary of the relationship between RSI and day of the week. Hint: you will need to create a new variable for day of the week.

1b: Adjusted Model and Interpretation

Adjusting for the effect of moon phase, what is the adjusted estimate for the association between RSI and day of the week? Write a brief, but complete, summary of the relationship between RSI and day of the week adjusting for moon phase.

1c: Moon Phase Confounding

Is moon phase a confounder of the association between RSI and day of the week based on the operational criterion? Should you report the results from (A) or (B)? Justify your answer.

Exercise 2: Mediation

2a: Mediation DAG

Fit the three fundamental models of mediation analysis and fill in the following DAG:

2b: Percent Mediated

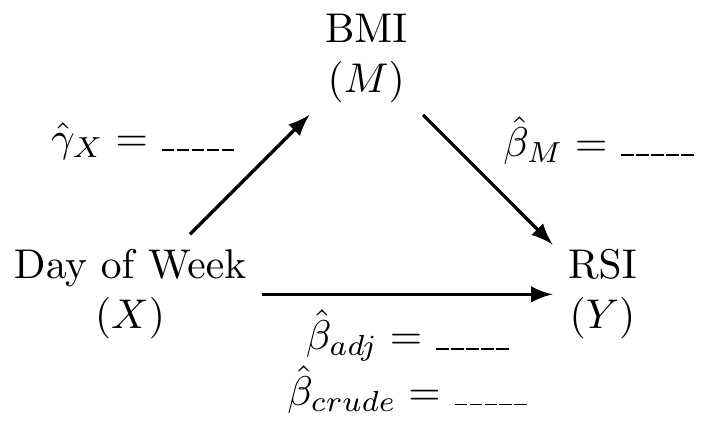
What is the proportion/percent mediated by age?

2c: 95% CI for Percent Mediated

What is the 95% CI and corresponding p-value for the proportion/percent mediated by age using the normal approximation to estimate the standard error (i.e., Sobel’s test)?

Exercise 3: Interactions

Use linear regression to examine the relationship between RSI for in-hospital complications and BMI. In this exercise you will examine whether the magnitude of the association between RSI (the response) and BMI (the primary explanatory variable) depends on whether the patient has diabetes.

3a: Fitted Regression Equation with Interaction

Write down the fitted regression equation for the regression of RSI on BMI, diabetes, and the interaction between the two. Provide an interpretation for each of the coefficients in the model (including the intercept).

3b: Interaction Test

Test whether the relationship between RSI and BMI depends on whether the patient had diabetes.

3c: Fitted Regression Model for Patients without Diabetes

What is the regression equation for patients who don’t have diabetes?

3d: Fitted Regression Model for Patients with Diabetes

What is the regression equation for patients with diabetes?

3e: Interaction Visualization

Create a scatterplot of RSI versus BMI, using different symbols and separate regression lines for patients with and without diabetes.

3f: Hypothesis Test for BMI without Diabetes

Test if the slope for BMI for those who don’t have diabetes is significantly different from 0.

3g: Hypothesis Test for BMI with Diabetes

Test if the slope for BMI for those who do have diabetes is significantly different from 0.

3h: Interactions and Brief, but Complete, Summaries

Provide a brief, but complete, summary of the relationship between RSI and BMI, accounting for any observed interaction with diabetes (i.e., if there is a significant interaction, interpret those who do and don’t have diabetes separately).

Exercise 4: Polynomial Regression

For this exercise, subset the data set to only those with an in-hospital complication recorded and those who have hip replacements (i.e., dat$ahrq_ccs=='Hip replacement; total and partial').

4a: SLR

Fit a simple linear regression model for the outcome of RSI for in-hospital complications with age as the predictor.

4b: Polynomial Regression

Fit a polynomial regression model that adds a squared term for age.

4c: Polynomial Plots

Create a scatterplot of the data and add the predicted regression lines for each model.

4d: Polynomial vs SLR

Based on the model output and figure, is there evidence that a quadratic model may be more appropriate than the simple linear regression model?

Exercise 5: Tests of General Linear Hypotheses

5a: Fitting The Model

Fit a linear regression model for the outcome of RSI for in-hospital complication with day of the week as a predictor for all days.

5b: GLHT for Two Coefficients

Using a general linear hypothesis, test if the mean RSI on Tuesday and Wednesday are equal to each other.

5c: GLHT for Combination of Coefficients

Using a general linear hypothesis, test if the mean RSI on Monday is equal to two times the RSI on Thursday.

5d: GLHT for Simultaneous Testing

Using a general linear hypothesis, test both 5b and 5c simultaneously.

--- title: "Week 11 Practice Problems" author: name: Alex Kaizer roles: "Instructor" affiliation: University of Colorado-Anschutz Medical Campus toc: true toc_float: true toc-location: left format: html: code-fold: show code-overflow: wrap code-tools: true --- ```{r, echo=F, message=F, warning=F} library(kableExtra) library(dplyr) ``` This page includes optional practice problems, many of which are structured to assist you on the homework with [Solutions provided on a separate page](/labs/prac11s/index.qmd). Data sets, if needed, are provided on the BIOS 6618 Canvas page for students registered for the course. This week's extra practice exercises focus on the wonderfully wide world of applications for MLR: confounding, mediation, interactions, general linear hypothesis testing, and polynomial regression. # Dataset Background All of our exercises will use the surgery timing data set (`Surgery_Timing.csv`) provided by the TSHS section of the American Statistical Association. We can load the data into R with the following line of code: ```{r, eval=F} dat <- read.csv('../../.data/Surgery_Timing.csv') ``` The following table summarizes the variables we will be exploring and provide brief definitions: | Variable | Code Name | Description | |:--------------------------------------------------------------|:-----------------|:-----------------------------------------------------------------------------| | Risk Stratification Index (RSI) for In-Hospital Complications | `complication_rsi` | Estimated risk of having an in-hospital complication. | | Day of Week | `dow` | Weekday surgery took place (1=Monday, 5=Friday) | | Operation Time | `hour` | Timing of operation during the day (06:00 to 19:00) | | Phase of Moon | `moonphase` | Moon phase during procedure (1=new, 2=first quarter, 3=full, 4=last quarter) | | Age | `age` | Age in years | | BMI | `bmi` | Body mass index (kg/m2) | | AHRQ Procedure Category | `ahrq_ccs` | US Agency for Healthcare Research and Quality's Clinical Classifications Software procedure category | | Complication Observed | `complication` | In-hospital complication | | Diabetes | `baseline_diabetes` | Diabetes present at baseline | # Exercise 1: Confounding We will use linear regression to examine the relationship between the outcome of RSI for in-hospital complications with surgery on a Monday/Tuesday (versus Wednesday/Thursday/Friday) and moon phase to answer the following exercises: ## 1a: Unadjusted Model and Interpretation What is the unadjusted (crude) estimate for the association between RSI and day of the week? Write a brief, but complete, summary of the relationship between RSI and day of the week. *Hint: you will need to create a new variable for day of the week.* ## 1b: Adjusted Model and Interpretation Adjusting for the effect of moon phase, what is the adjusted estimate for the association between RSI and day of the week? Write a brief, but complete, summary of the relationship between RSI and day of the week adjusting for moon phase. ## 1c: Moon Phase Confounding Is moon phase a confounder of the association between RSI and day of the week based on the operational criterion? Should you report the results from (A) or (B)? Justify your answer. # Exercise 2: Mediation We will use linear regression to examine the relationship between the outcome of RSI for in-hospital complications with surgery on a Monday/Tuesday (versus Wednesday/Thursday/Friday) and BMI of the patient potential mediator to complete the following exercises: ## 2a: Mediation DAG Fit the three fundamental models of mediation analysis and fill in the following DAG: ```{tikz, tikz-med, fig.ext = 'png', cache=TRUE, echo=F, fig.align="center", fig.width=4} \usetikzlibrary{arrows} \begin{tikzpicture}[node distance=4cm, auto,>=latex, thick, scale = 0.5] \node (X) [align=center] {Day of Week \\ ($X$)}; \node (M) [align=center,above of=X,xshift=2cm,yshift=-2cm] {BMI \\ ($M$)}; \node (Y) [align=center,right of=X] {RSI \\ ($Y$)}; \draw[->] (X) to node [above left] {$\hat{\gamma}_{X}=\_\_\_\_\_$} (M); \draw[->] (M) to node [above right] {$\hat{\beta}_{M}=\_\_\_\_\_$} (Y); \draw[->] (X) to node [align=center,swap] {$\hat{\beta}_{adj}=\_\_\_\_\_$ \\ $\hat{\beta}_{crude}=\_\_\_\_\_$} (Y); \end{tikzpicture} ``` ## 2b: Percent Mediated What is the proportion/percent mediated by age? ## 2c: 95% CI for Percent Mediated What is the 95% CI and corresponding p-value for the proportion/percent mediated by age using the normal approximation to estimate the standard error (i.e., Sobel's test)? # Exercise 3: Interactions Use linear regression to examine the relationship between RSI for in-hospital complications and BMI. In this exercise you will examine whether the magnitude of the association between RSI (the response) and BMI (the primary explanatory variable) depends on whether the patient has diabetes. ## 3a: Fitted Regression Equation with Interaction Write down the fitted regression equation for the regression of RSI on BMI, diabetes, and the interaction between the two. Provide an interpretation for each of the coefficients in the model (including the intercept). ## 3b: Interaction Test Test whether the relationship between RSI and BMI depends on whether the patient had diabetes. ## 3c: Fitted Regression Model for Patients without Diabetes What is the regression equation for patients who don't have diabetes? ## 3d: Fitted Regression Model for Patients with Diabetes What is the regression equation for patients with diabetes? ## 3e: Interaction Visualization Create a scatterplot of RSI versus BMI, using different symbols and separate regression lines for patients with and without diabetes. ## 3f: Hypothesis Test for BMI without Diabetes Test if the slope for BMI for those who don't have diabetes is significantly different from 0. ## 3g: Hypothesis Test for BMI with Diabetes Test if the slope for BMI for those who do have diabetes is significantly different from 0. ## 3h: Interactions and Brief, but Complete, Summaries Provide a brief, but complete, summary of the relationship between RSI and BMI, accounting for any observed interaction with diabetes (i.e., if there is a significant interaction, interpret those who do and don't have diabetes separately). # Exercise 4: Polynomial Regression For this exercise, subset the data set to only those with an in-hospital complication recorded and those who have hip replacements (i.e., `dat$ahrq_ccs=='Hip replacement; total and partial'`). ## 4a: SLR Fit a simple linear regression model for the outcome of RSI for in-hospital complications with age as the predictor. ## 4b: Polynomial Regression Fit a polynomial regression model that adds a squared term for age. ## 4c: Polynomial Plots Create a scatterplot of the data and add the predicted regression lines for each model. ## 4d: Polynomial vs SLR Based on the model output and figure, is there evidence that a quadratic model may be more appropriate than the simple linear regression model? # Exercise 5: Tests of General Linear Hypotheses ## 5a: Fitting The Model Fit a linear regression model for the outcome of RSI for in-hospital complication with day of the week as a predictor for all days. ## 5b: GLHT for Two Coefficients Using a general linear hypothesis, test if the mean RSI on Tuesday and Wednesday are equal to each other. ## 5c: GLHT for Combination of Coefficients Using a general linear hypothesis, test if the mean RSI on Monday is equal to two times the RSI on Thursday. ## 5d: GLHT for Simultaneous Testing Using a general linear hypothesis, test both 5b and 5c simultaneously.