Classical Criteria of Confounding
This page is part of the University of Colorado-Anschutz Medical Campus’ BIOS 6618 Recitation collection. To view other questions, you can view the BIOS 6618 Recitation collection page or use the search bar to look for keywords.
Classical Criteria of Confounding
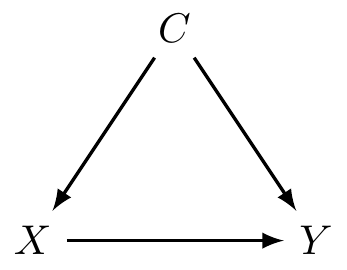
From our DAG, we can define three models of interest:
Crude Model: \(\hat{Y} = \hat{\beta}_{01} + \hat{\beta}_{crude}X\)
Adjusted Model: \(\hat{Y} = \hat{\beta}_{02} + \hat{\beta}_{adj}X + \hat\beta_{C}C\)
Covariate Model: \(\hat{C} = \hat{\gamma}_{0} + \hat{\gamma}_{X}X\)
We will use these three models to evaluate potential confounders.
The classical criteria for confounding is comprised of 3 considerations:
A confounding factor must be associated with the exposure (or PEV) under study. From our three models, this is the association of \(X\) and \(C\) represented by \(\hat{\gamma}_{X}\).
A confounding factor must be a risk factor or a surrogate for a risk factor for the disease. From our three models, this is the association of \(C\) and \(Y\) given \(X\) represented by \(\hat{\beta}_{C}\).
A confounding factor must not be affected by the exposure or the disease. This one is based on the context/understanding.
There is also a separate operational criterion of confounding where confounding is present if there is a “meaningful” difference between \(\hat{\beta}_{crude}\) and \(\hat{\beta}_{adj}\), which will depend on the context and what would represent a clinically relevant change.
If clinically meaningful change is uncertain, we might calculate the percent change in one of two ways:
\(\frac{\hat{\beta}_{crude} - \hat{\beta}_{adj}}{\hat{\beta}_{crude}} \times 100\) (favored by biostatisticians)
\(\frac{\hat{\beta}_{crude} - \hat{\beta}_{adj}}{\hat{\beta}_{adj}} \times 100\) (favored by epidemiologists)
In both cases we need to rely on knowledge of the subject area to determine if the arrows in our DAG are indicating that the variable under considering is a confounder (and not a mediator, etc.).