Creating ROC Curves from Tabular Data

Author

Affiliation

Alex Kaizer

University of Colorado-Anschutz Medical Campus

This page is part of the University of Colorado-Anschutz Medical Campus’ BIOS 6618 Recitation collection. To view other questions, you can view the BIOS 6618 Recitation collection page or use the search bar to look for keywords.

Calculating the ROC Curve from Tabular Data

In some cases, we may be asked to create an ROC curve from tabular data. Our first step is that we need to convert the tabular data into a long format dataset (i.e., one and only one row per each participant represented in the table). There are a few ways we can approach this problem, here we will review two strategies using a different made up prospective Cohort study for diagnosing Celiac disease based on the Tissue Transglutaminase IgA antibody (tTG-IgA):

tTG-IgA Range	Not Celiac	Celiac
<4	841	2
4-10	22	3
> 10	0	9

Strategy 1: Create a Data Frame Manually

If we haven’t been given any of the data in tabular form yet, it may be just as easy to create a data frame directly:

Code

celiac_df <- data.frame(
  celiac = c(rep(0,863), rep(1,14)), # create variable for disease status
  ttg = c(rep(0,841),rep(4,22), rep(0,2),rep(4,3),rep(10,9)) # create variable for tTG value
)

Then we can see that using pROC::roc we can generate a receiver operating characteristic curve and calculated its AUC:

Code

celiac_roc <- pROC::roc( celiac ~ ttg, data=celiac_df )

Setting levels: control = 0, case = 1

Setting direction: controls < cases

Notice how the output tells us which celiac group is assumed to be the controls and the cases. This can be helpful to check that we have the right classifications for our interpretations. It also tells us which directionality of the numeric ttg is being used for classification (i.e., specifically that values below a threshold are assumed to predict controls and values above the threshold to predict cases).

Code

library(pROC)
plot(celiac_roc, print.auc=TRUE,print.auc.x=1, print.auc.y=1)

Code

auc(celiac_roc)

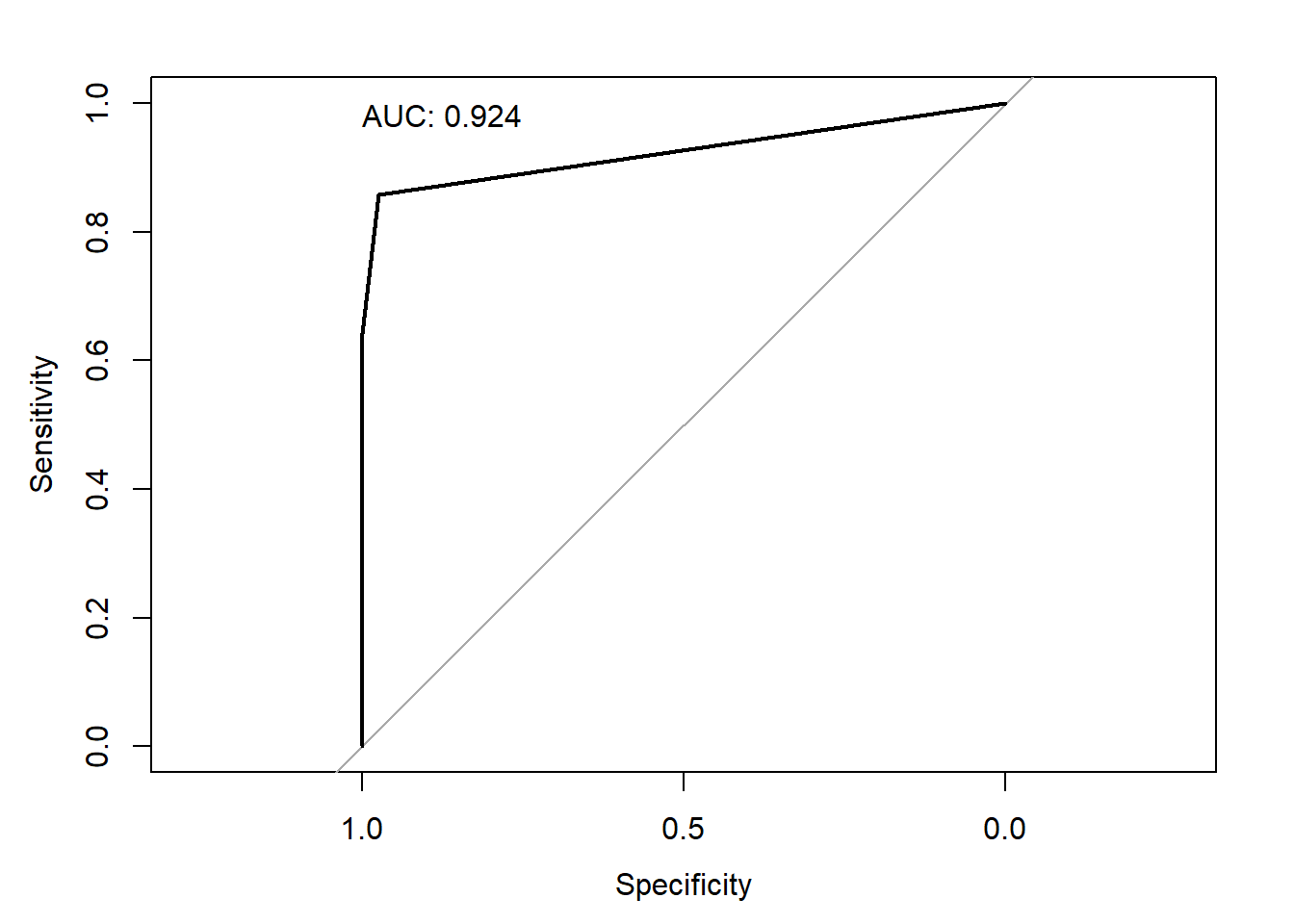
Area under the curve: 0.924

With only 3 thresholds (i.e., 0, 4, and 10) it isn’t the most exciting ROC curve, but we do see that its high AUC suggests tTG as a predictive tool to identify Celiac disease is better than random chance.

Strategy 2: Convert a Contingency Table to a Data Frame

Another option is to use some combination of functions to manipulate an existing contingency table of the $N$’s in each group. Here we see how we can use reshape2::melt and splitstackshape::expandRows:

Code

# Step 1: create a table of the information, here we'll just make it as a matrix object
celiac_mat <- matrix( c(841,22,0,2,3,9), ncol=2, byrow=FALSE, dimnames=list(c('<4','4-10','>10'), c('Not Celiac','Celiac')))

celiac_mat

     Not Celiac Celiac
<4          841      2
4-10         22      3
>10           0      9

Code

# Step 2: convert to a data frame
library(reshape2)
library(splitstackshape)

celiac_melt <- melt(celiac_mat)
celiac_melt

  Var1       Var2 value
1   <4 Not Celiac   841
2 4-10 Not Celiac    22
3  >10 Not Celiac     0
4   <4     Celiac     2
5 4-10     Celiac     3
6  >10     Celiac     9

Code

celiac_df2 <- expandRows(celiac_melt, 'value')

The following rows have been dropped from the input: 

3

Code

dim(celiac_df2)

[1] 877   2

Code

celiac_df2[c(1,100,500,850,867,877),]

      Var1       Var2
1       <4 Not Celiac
1.99    <4 Not Celiac
1.499   <4 Not Celiac
2.8   4-10 Not Celiac
5.1   4-10     Celiac
6.8    >10     Celiac

For the pROC::roc function, we need to convert this into a numeric format. We should also create a column for Celiac to avoid the function having to induce a logical outcome of TRUE or FALSE based on just the character string alone (i.e., being explicit helps us avoid unknown R defaults that might affect our results). One approach is to create new columns and leverage which() statements:

Code

# Create column for numeric version of tTG variable where we set lower limit as value
celiac_df2$ttg <- NA
celiac_df2$ttg[which(celiac_df2$Var1 == '<4')] <- 0
celiac_df2$ttg[which(celiac_df2$Var1 == '4-10')] <- 4
celiac_df2$ttg[which(celiac_df2$Var1 == '>10')] <- 10

# Create column for logical indicator of Celiac
celiac_df2$celiac <- celiac_df2$Var2=='Celiac'

With a numeric variable, we can generate the ROC curve and calculate the AUC:

Code

celiac_roc2 <- pROC::roc( celiac ~ ttg, data=celiac_df2 )

Setting levels: control = FALSE, case = TRUE

Setting direction: controls < cases

Code

plot(celiac_roc2, print.auc=TRUE,print.auc.x=1, print.auc.y=1)

Code

auc(celiac_roc2)

Area under the curve: 0.924

--- title: "Creating ROC Curves from Tabular Data" author: name: Alex Kaizer roles: "Instructor" affiliation: University of Colorado-Anschutz Medical Campus toc: true toc_float: true toc-location: left format: html: code-fold: show code-overflow: wrap code-tools: true --- ```{r, echo=F, message=F, warning=F} library(kableExtra) library(dplyr) ``` This page is part of the University of Colorado-Anschutz Medical Campus' [BIOS 6618 Recitation](/recitation/index.qmd) collection. To view other questions, you can view the [BIOS 6618 Recitation](/recitation/index.qmd) collection page or use the search bar to look for keywords. # Calculating the ROC Curve from Tabular Data In some cases, we may be asked to create an ROC curve from tabular data. Our first step is that we need to convert the tabular data into a long format dataset (i.e., one and only one row per each participant represented in the table). There are a few ways we can approach this problem, here we will review two strategies using a different made up prospective Cohort study for diagnosing Celiac disease based on the Tissue Transglutaminase IgA antibody (tTG-IgA): | tTG-IgA Range | Not Celiac | Celiac | |:--------------|:----------:|:------:| | <4 | 841 | 2 | | 4-10 | 22 | 3 | | > 10 | 0 | 9 | ## Strategy 1: Create a Data Frame Manually If we haven't been given any of the data in tabular form yet, it may be just as easy to create a data frame directly: ```{r} celiac_df <- data.frame( celiac = c(rep(0,863), rep(1,14)), # create variable for disease status ttg = c(rep(0,841),rep(4,22), rep(0,2),rep(4,3),rep(10,9)) # create variable for tTG value ) ``` Then we can see that using `pROC::roc` we can generate a receiver operating characteristic curve and calculated its AUC: ```{r, warning=F} celiac_roc <- pROC::roc( celiac ~ ttg, data=celiac_df ) ``` Notice how the output tells us which `celiac` group is assumed to be the controls and the cases. This can be helpful to check that we have the right classifications for our interpretations. It also tells us which directionality of the numeric `ttg` is being used for classification (i.e., specifically that values below a threshold are assumed to predict controls and values above the threshold to predict cases). ```{r, message=F} library(pROC) plot(celiac_roc, print.auc=TRUE,print.auc.x=1, print.auc.y=1) auc(celiac_roc) ``` With only 3 thresholds (i.e., 0, 4, and 10) it isn't the most exciting ROC curve, but we do see that its high AUC suggests tTG as a predictive tool to identify Celiac disease is better than random chance. ## Strategy 2: Convert a Contingency Table to a Data Frame Another option is to use some combination of functions to manipulate an existing contingency table of the $N$'s in each group. Here we see how we can use `reshape2::melt` and `splitstackshape::expandRows`: ```{r} # Step 1: create a table of the information, here we'll just make it as a matrix object celiac_mat <- matrix( c(841,22,0,2,3,9), ncol=2, byrow=FALSE, dimnames=list(c('<4','4-10','>10'), c('Not Celiac','Celiac'))) celiac_mat ``` ```{r, warning=FALSE} # Step 2: convert to a data frame library(reshape2) library(splitstackshape) celiac_melt <- melt(celiac_mat) celiac_melt celiac_df2 <- expandRows(celiac_melt, 'value') dim(celiac_df2) celiac_df2[c(1,100,500,850,867,877),] ``` For the `pROC::roc` function, we need to convert this into a numeric format. We should also create a column for Celiac to avoid the function having to induce a logical outcome of TRUE or FALSE based on just the character string alone (i.e., being explicit helps us avoid unknown R defaults that might affect our results). One approach is to create new columns and leverage `which()` statements: ```{r} # Create column for numeric version of tTG variable where we set lower limit as value celiac_df2$ttg <- NA celiac_df2$ttg[which(celiac_df2$Var1 == '<4')] <- 0 celiac_df2$ttg[which(celiac_df2$Var1 == '4-10')] <- 4 celiac_df2$ttg[which(celiac_df2$Var1 == '>10')] <- 10 # Create column for logical indicator of Celiac celiac_df2$celiac <- celiac_df2$Var2=='Celiac' ``` With a numeric variable, we can generate the ROC curve and calculate the AUC: ```{r, warning=F} celiac_roc2 <- pROC::roc( celiac ~ ttg, data=celiac_df2 ) plot(celiac_roc2, print.auc=TRUE,print.auc.x=1, print.auc.y=1) auc(celiac_roc2) ```